Estimation

Lecture Notes on Causal Inference

Preliminaries

在之前的内容中，我们通过indentification，将Causal Estimand转换为Statistical Estimand，即 $P(Y\vert do(t)) \rightarrow P(Y\vert t)$ 。接下来在本章的部分，我们进行的是下一阶段，对Statistical Estimand $P(Y\vert t)$ 进行估计。在Estimation中，我们输入数据，得到预测结果

此外，我们还需要引入一个新的概念Conditional average treatment effects (CATEs)，和之前讲过的ATE相比，多了一个条件，记为

\[\tau(x) \triangleq E[Y(1)-Y(0)\vert X=x]\]

按与之类似的写法，之前的ATE可以表示为

\[\tau \triangleq E[Y(1)-Y(0)]\]

在该公式中，X不一定必须是观测变量，尽管通常都是。

Conditional outcome modeling (COM)

展开我们之前写出的ATE的公式，我们可以得到熟悉的
\(\tau = E_W [E[Y \vert T = 1, W] - E[Y \vert T = 0, W]]\)
在estimation阶段，我们需要对$E[Y \vert T = 1, W]$进行建模，为了方便，我们重写ATE的公式

\[\tau = E_W [\mu(1,W) - \mu(0,W)]\]

这里的 $\mu(1,W)$ 和 $\mu(0,W)$ 即为我们的建模(比如利用DNN，则这里表示两个网络模型)。接下来我们需要对W近似，因为可能其维度太高，数据太多，无法得到准确的期望值，此时近似后的ATE我们称为ATE COM Estimator，即

\[\hat{\tau} = \frac{1}{n} \sum_i(\hat{\mu}(1,w_i) - \hat{\mu}(0,w_i))\]

同理，对于CATE，我们也是首先定义$\mu$来方便表示我们建立的模型，因为包含条件概率，我们记作

\[\mu(t,w,x)\triangleq E[Y\vert T=t,W=w,X=x]\]

再对W进行近似，得到近似后的 $\hat{\tau(x)}$，我们称为CATE COM Estimator，即

\[\hat{\tau}(x) = \frac{1}{n_x} \sum_{i:x_i=x}(\hat{\mu}(1,w_i,x) - \hat{\mu}(0,w_i,x))\]

COM还有一些其它的称呼，比如G-computation estimators、Parametric G-formula、Standardization and S-learner where “S” is for “Single”

但现在存在一个问题，此时模型的输入为 W 和 T，W 为高维数据，T为一维数据。大量从 T 出来的权值都为0或极小值，对结果的影响几乎为零。该问题称为 estimate can be biased toward zero，那么我们应该怎么做来让模型不再忽略 T 的作用呢，由此我们引出Grouped COM (GCOM)

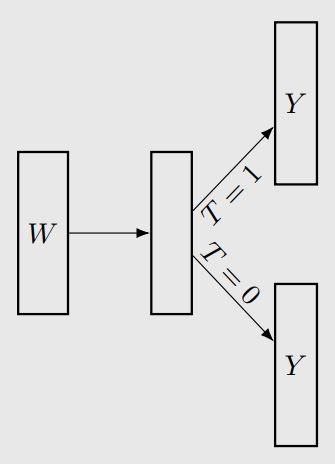
在 GCOM 下，我们用两个网络(模型)分别去模拟T=0和T=1的情况，此时T信息就被隐含地编码的不同网络中了，此时可以写出对应的GCOM Estimator，即

\[\hat{\tau} = \frac{1}{n} \sum_i(\hat{\mu}_1(w_i) - \hat{\mu}_0(w_i))\]

对于T=1的网络，我们称为treatment group，就只用包含T=1的数据训练；同样，对于T=0的网络，我们称为control group，只用包含T=0的数据训练。这又引出了新的问题，这样数据的利用效率是很低的，我们应该如何提升利用效率呢？

Increasing Data Efficiency

Propensity scores

我们定义Propensity scores e(w)为 $e(w)\triangleq P(T=1 \vert W)$
我们可以发现，无论 W 是多少维的数据，其Propensity scores e(w)永远是一维数据。基于Propensity scores，我们有一个定理

\[(Y(1),Y(0)) \perp \!\!\! \perp T\vert W \Rightarrow (Y(1),Y(0)) \perp \!\!\! \perp T\vert e(W)\]

这个定理成立是因为condition on W 时，我们相当于移除因果图中 W 这个节点，使Y与T独立。而condition on e(W)时，我们相当于移除因果图中 W 到 T 的所有边，这样block掉了所有的backdoor path，同样得到独立

为此我们想到了Positivity-Unconfoundedness Tradeoff，我们能不能用e(W)去代替W实现降维呢？这样的话overlap的程度就会更高。

但这样是不行的，因为我们无法得到 $P(T=1 \vert W)$，在实际中，最好的方式是对其建模，把降维问题转化为对e(W)的建模问题

Inverse probability weighting (IPW)

在介绍IPW之前，我们首先说明一下应用背景。在经典的(T,W,Y)三元例子中，correlation并不等于causality，即 $P(T\vert W)\neq P(T)$ ，这也导致我们无法分析T与Y的causal effect。但是如果 $P(T\vert W)= P(T)$ 或者是 $P(T\vert W)=1$ ，则此时 T 与 Y 之间就只存在因果关系，没有其他关系了。为了实现这种情况，我们可以对 $P(T\vert W)$ 这一项除以相同大小的值，即可将其变为1。由此引出 IPW

在IPW中，我们对 Y 这一变量进行处理，此时 $E[Y(t)]=E[\frac{1(T=t)Y}{p(t\vert W)}]$ ，ATE的公式也随之发生改变，即

\[\tau \triangleq E[Y(1)-Y(0)] = E[\frac{1(T=1)Y}{e(W)}] - E[\frac{1(T=0)Y}{1-e(W)}]\]

对 W 近似后的公式为

\[\hat{\tau} = \frac{1}{n_1} \sum_{i:t_i=1}\frac{y_i}{\hat{e}(w_i)} - \frac{1}{n_0} \sum_{i:t_i=0}\frac{y_i}{1-\hat{e}(w_i)}\]

在CATE estimation下应该如何应用呢？这超出了课程范围，可以阅读参考文献
https://www.tandfonline.com/doi/full/10.1080/07350015.2014.975555

Other Methods

这里简要介绍一些其他的建模估计方法