Identification

Lecture Notes on Causal Inference

Random Experience

之前已经讲过 random experience 的原理和背景，这里尝试从不同的角度去解释该方法的神奇之处。在 random experience 中，对比的两组除了treatment，其它均相同。

  1. Covariate balance：在这里我们定义为不同 treatment 下的变量X的分布相同，则称为具有 covariate balance，从数学公式的角度来看，即 \(P(X \vert T = 1) = P(X \vert T = 0)\)。
    在定义该概念之后，我们可以从 random experience 得到 covariate balance，进而从 covariate balance 得到因果关系
    1. 首先根据random experience，我们可以得到 T 与 X 相互独立(这是因为 T 是通过抛硬币的方式确定的)，因此我们可以得到 covariate balance
    2. 基于 covariate balance，我们可以推出因果关系，\(P(y\vert do(t))=\sum_x P(y\vert x,t)P(x)=\sum_x \frac{P(y\vert x,t)P(x)P(t\vert x)}{P(t\vert x)} = \sum_x P(x,y\vert t) = P(y\vert t)\)
  2. Exchangeability：这个在之前讲过，是说我们可以交换采取不同措施的两组人，而结果不发生改变
  3. No backdoor paths：随机实验切断了所有指向 treatment 的原因线，no edges to T

Frontdoor adjustment

在介绍frontdoor之前，首先回顾一下backdoor。backdoor path是说因果图中非chain的association path，即存在edge由x指向t，同时存在从x到y的路径。此时我们称存在backdoor path。backdoor关注的是非因果关系的其它关系。

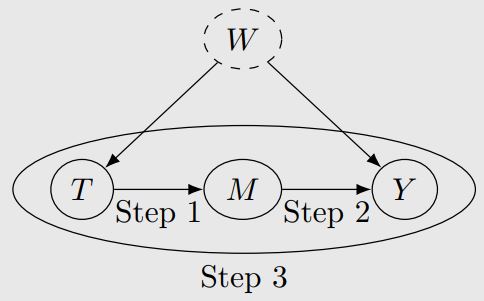
然而，在平常的观测数据中，存在未知的潜在原因，我们不能用backdoor那一套方法对潜在原因去condition，此时我们可以做的，就是关注因果关系路径上的中间节点，而这也就是 frontdoor 的来源。frontdoor是为了聚焦chain形式的因果关系。举个例子，假设一个因果关系是 T 到 M 到 Y，那么在分析 T 与 Y 的因果关系时，我们就可以利用 frontdoor 来关注中间原因 M。

frontdoor adjustment 总共包含三步，以上述例子为例

  1. Identify the causal effect of T on M
    在 T 和 M 之间，不存在backdoor path，因为此时 Y 是未知的，作为collider，切断了未知原因 W 对 M 的影响。此时我们有 \(P(m \vert do(t)) = P(m \vert t)\)

  2. Identify the causal effect of M on Y
    在 M 和 Y 之间，存在一条backdoor path，从 T 流向 W 流向 Y。因此我们需要condition on T 来阻塞这条关系路径。此时我们有 \(P(y \vert do(m)) = \sum_t P(y \vert m,t)P(t)\)
  3. Combine above two steps
    \(P(y | do(t)) = \sum_m P(m | do(t)) P(y | do(m)) =\sum_m P(m | t)\sum_{t'}P(y \vert m,t')P(t')\)

经过这三步，我们就得到了关于 (T, M, Y) 三元组的 frontdoor adjustment。这就引出了下一个问题，在复杂的图中，如何确定 M 呢？于是我们提出 frontdoor criterion。

对于一组变量 M ，确定其满足 frontdoor criterion 需要同时满足三个条件

  1. M 挡住所有从 T 到 Y 的因果路径
  2. T 到 M 之间，所有的backdoor path 都应该是阻塞的。
  3. M 到 Y 之间，所有的backdoor path 都被 T 阻塞

Pearl’s do-calculus

当 frontdoor 和 backdoor criterion 都无法满足的时候，我们该如何 indentify causal effect呢？此时我们可以用do-calculus。

do-calculus可以indentify任何indentifiable的causal quantity。换句话是，它是完备的(complete)

在介绍do-calculus之前，需要引入一个新的记号。对于一个因果图G，我们用 \(G_{\overline Z}\) 表示将G图中所有指向节点 Z 的边都抹去后剩下的图；同理，我们用 \(G_{\underline{Z}}\) 表示将G图中所有从节点 Z 指出的边都抹去后剩下的图。

do-calculus有三条rule

  1. \[P(y\vert do(t),z,w)=P(y\vert do(t),w)\qquad if\ Y\perp \!\!\! \perp _{G_{\overline{T}}} Z\vert T,W\]

    如果去掉do(t)，我们可以发现这条规则是 d-seperation 和条件独立的泛化

  2. \[P(y\vert do(t),do(z),w)=P(y\vert do(t),z,w)\qquad if\ Y\perp \!\!\! \perp_{G_{\overline{T},\underline{Z}}} Z\vert T,W\]

    如果去掉do(t)，我们可以发现这条规则是 backdoor adjustment 的泛化，此时Z没有指出的边，do on z 不会对其他变量产生影响

  3. \[P(y\vert do(t),do(z),w)=P(y\vert do(t),w)\qquad if\ Y\perp \!\!\! \perp_{G_{\overline{T},\overline{Z(W)}}} Z\vert T,W\]

    这里Z(W)表示所有Z中所有不是W父节点的节点集合
    如果去掉do(t)，我们可以发现在 \(G_{\overline{Z(W)}}\) 中，只有 z->y 可能有因果关系，w被抹除了，其效果和 \(G_{\overline{Z}}\)相同。但 \(G_{\overline{Z}}\)更严格，会有更多的边被抹去，可能会丢失一些association

Determining identifiability from the graph