The Flow of Association and Causation in Graphs
Lecture Notes on Causal Inference
Bayesian networks and causal graphs
对联合分布最直接的建模(no causality),将联合分布展开为条件概率的乘积,再结合data table建模,即 \(P(x_1,x_2,...,x_n) = P(x_1)\prod_iP(x_i\vert x_{i-1},...,x_1)\) 但显然这种方法太暴力,需要的参数太多。
为此,我们引入 Local Markov assumption,该假设是说,在有向无环图 (DAG)中,对于某节点X,若我们给出的它的父节点,则该节点和所有其它的非子代节点独立。由此,我们可以得到贝叶斯网络的分解,即 \(P(x_1,x_2,...,x_n) = \prod_iP(x_i\vert parent(x_i))\) 可以证明,\(Local\ Markov\ assumption \Longleftrightarrow Bayesian\ network\ factorization\)
但是,仅仅只有 Local Markov assumption还不够,因为它没有给出dependent的关系约束。为了避免该假设带来的歧义,我们引入了 Minimality assumption。 具体来说,Minimality assumption 包含了两条假设,第一条和Local Markov assumption一致,第二条是说,有向无环图中,相邻节点之间是dependent的关系。
此外,我们还引入了 Causal edges assumption,该假设是说,在有向图中,每一个父节点都是所有其子节点的直接原因。
综上所述,所有假设的逻辑关系如下
- 通过Markov Assumption,我们得到数据间的Independency关系
- 通过Minimality Assumption,我们得到数据间的Dependency关系
- 通过Causal Edges Assumption,我们得到Causal Dependencies关系
Graphical building blocks
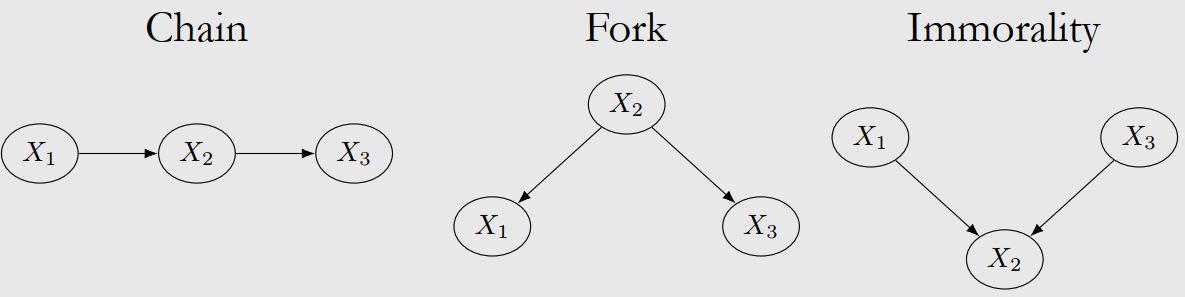
在这里,我们主要讨论三种最基本的blocks形式。
-
Chain
\(X_1\)与\(X_3\)之间存在association的关系,但是如果我们已知\(X_2\),则此时\(X_1\)与\(X_3\)相互独立,即\(P(x_1, x_3 \vert x_2) = P(x_1 \vert x_2) P(x_3 \vert x_2)\)。证明如下
根据贝叶斯网络展开,\(P(x_1,x_2,x_3) = P(x_1)P(x_2 \vert x_1)P(x_3 \vert x_2)\)
应用贝叶斯公式,\(P(x_1, x_3 \vert x_2) = P(x_1, x_2, x_3)/P(x_2)\)
综合以上两式,可得到 \(P(x_1, x_3 \vert x_2) = P(x_1 \vert x_2) P(x_3 \vert x_2)\) -
Fork
与chain类似,\(P(x_1, x_3 \vert x_2) = P(x_1 \vert x_2) P(x_3 \vert x_2)\)证明如下
根据贝叶斯网络展开,\(P(x_1,x_2,x_3) = P(x_2)P(x_1 \vert x_2)P(x_3 \vert x_2)\)
应用贝叶斯公式,\(P(x_1, x_3 \vert x_2) = P(x_1, x_2, x_3)/P(x_2)\)
综合以上两式,可得到 \(P(x_1, x_3 \vert x_2) = P(x_1 \vert x_2) P(x_3 \vert x_2)\) -
Immorality
在未知\(X_2\)时,\(X_1\)与\(X_3\)本身就是相互独立的关系,此时为blocked path。即 \(P(x_1,x_3) = P(x_1)P(x_3)\)。证明如下
根据贝叶斯网络展开,\(P(x_1,x_2,x_3) = P(x_1)P(x_3)P(x_2 \vert x_1,x_3)\)
应用概率论知识,\(P(x_1, x_3) = \sum_{x_2}P(x_1,x_2,x_3)\)
综合以上两式,可得到 \(P(x_1, x_3) = P(x_1)P(x_3)\)然而,当我们知道\(X_2\)后,\(X_1\)与\(X_3\)又失去了独立性。如果我们block \(X_2\),则会使\(X_1\)与\(X_3\)产生association关系,\(X_2\)这样的节点又被称为collider
综上所述,在 Chain 和 Fork 中,Condition on \(X_2\) blocks a path;在 Immorality 中,path is blocked originally.
Flow of association and causation
引入概念 d-separation
对于两组点X和Y,如果存在另外一组点Z,使得X和Y之间所有的路径都被阻塞,则此时称 X and Y are d-separated
只有Chain form对应causal association,其他形式对应non-causal association(如 confounding association)