Potential Outcome

Lecture Notes on Causal Inference

Average treatment effect (ATE)

用平均的方式替代个体，来解决causal effect无法得到的问题。即\(E_i[Y_i(1)-Y_i(0)]\)，通常我们省略下标i，写作\(E[Y(1)-Y(0)]\) 其中，最关键的一点是：

\[E[Y(1)-Y(0)] = E[Y(1)]-E[Y(0)] \neq E[Y|T=1]-E[Y|T=0]\]

最后一项被称为associational difference。正如之前所解释的那样，不等关系源自两组数据间的不可比性。那么什么样的数据是可比的呢？还是以穿鞋睡觉与起床头疼为例，如果我们以上床前穿鞋与否进行划分，则此时两组人内清醒与醉酒的数量接近，是可比的。

Assumption for ATE = associational difference

• 第一条假设称为 Ignorability: \((Y(0),Y(1))\) are independent of T
  根据这条假设，我们可以得到

\[E[Y(1)-Y(0)] = E[Y(1)|T=1]-E[Y(0)|T=0]\]

为什么称为 ignorability呢？这是因为基于这条假设，我们可以忽略掉潜在原因对 T 和 Y 的影响(主要是对 T 的影响)
该假设的另一个解释角度，称为 exchangeability。意思是说，在我们交换 T 不同的两组人之后，结果仍然保持不变，即

\[E[Y(1)\vert T=1] = E[Y(1)\vert T=0] = E[Y(1)]\]

我们之所以想把 causal quantities (e.g. \(E[Y(1)]\)) 变成 statistical quantities (e.g. \(E[Y\vert T=1]\))，就是因为后者可以从 P(x,t,y) 的联合概率分布中得到，由此引出 identifiability的概念。
我们称一个 causal quantities (e.g. \(E[Y(t)]\))是 identifiable，如果它可以由statistical quantities (e.g. \(E[Y\vert t]\))计算得到

• 第二条假设与之类似，Conditional exchangeability: \((Y(0),Y(1))\) are independent of T given X
  根据这条假设，我们可以得到

\[E[Y(1)-Y(0)\vert X] = E[Y(1)|T=1,X]-E[Y(0)|T=0,X]\]

结合我们之前得到的ATE形式，我们可以得到修改后的版本，即identification of ATE

\[E[Y(1)-Y(0)] = E_XE[Y(1)-Y(0)\vert X] = above\ formula\]

此外，该假设还有很多不同称呼，unconfoundedness、conditional ignorability、 conditional exchangeability等。
这是一条无法被验证的假设，因为我们不能保证没有其他潜在原因影响 T 与 Y，若存在这样一个潜在原因，则此时该假设不成立。

• 第三条假设是 Positivity: \(0<P(T=1\vert X=x)<1\)
  这是一条我们必须保证的性质，因为我们可以把条件概率用贝叶斯拆开，此时Positivity对应的那一项出现在分母，我们需要避免除零的情况。
  对该性质的理解，有两种理解方式
  • 第一种是直觉上，假如 \(P(T=1\vert X=x)=1\)，则说明在 x 原因的作用下，所有人都采取了T=1的方式，那么此时我们无法分析Y与T的关系
  • 第二种是overlap的角度，我们画出 \(P(x\vert t)=1\) 与 x 的坐标图，对T=0和T=1分别绘图，如果两部分没有重叠，则说明严重违反了 Positivity性质。

Positivity-Unconfoundedness 存在tradeoff的关系，当维度越多，overlap的面积就越小
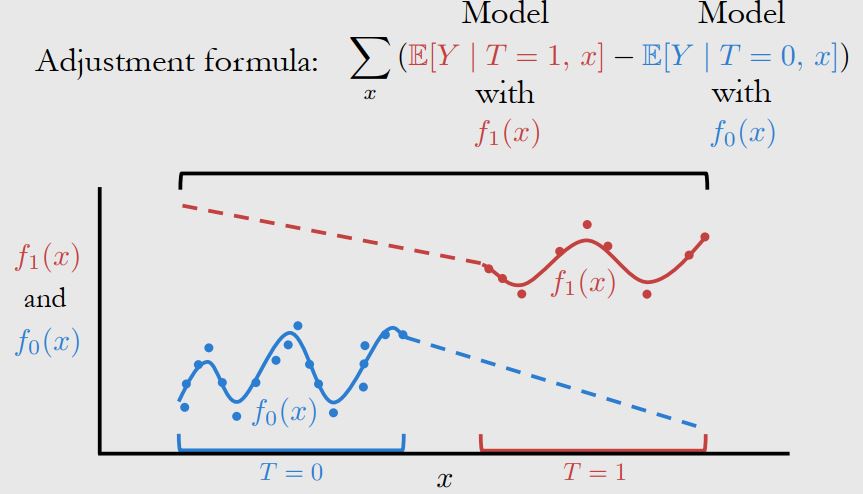
如果我们真的违反了 Positivity性质会发生什么？Extrapolation

• 第四条假设是 No interference: 其他个体采取的措施对当前个体的观测结果无影响，即

\[Y_i(t_1, . . . , t_{i-1}, t_i, t_{i+1}, . . . , t_n) = Y_i(t_i)\]

举例来说，如果我养一条狗会开心，那么其他人养狗则不会对我的心情产生影响

• 最后一条假设是 Consistency：当我们采取措施 T=t 时，观察到的结果就是潜在结果Y(t)，即

\[T=t \Longrightarrow Y=Y(t)\]

这个假设看起来是非常直觉的。举例来说，用 T=1 表示养一条狗，T=0 表示不养狗；同时，我养白狗会开心，养黑狗不开心，那么此时 Consistency 假设就被违反了。违反的原因来自举措 T 定义的不严谨

Tying it all together

在这里，我们结合之前提到的所有假设，对 causal effect 进行操作变形。

1. 为解决因果分析的根本问题，我们用ATE代替个人，并省略下标i，即

   \[E_i[Y_i(1) - Y_i(0)] = E[Y (1)-Y (0)]\]

2. 根据期望的线性性质和基本原理，将Causal estimand转换为Statistical estimand，即

   \[E_i[Y_i(1) - Y_i(0)] = E_X[E[Y (1) \vert X] - E[Y (0) \vert X]]\]

3. 根据 unconfoundedness 和 positivity 假设，增加 T 因素，即

   \[E_i[Y_i(1) - Y_i(0)] = E_X[E[Y (1) \vert T=1, X] - E[Y (0) \vert T=0, X]]\]

4. 根据 consistency 假设，进一步化简，得到最终形式，即

   \[E_i[Y_i(1) - Y_i(0)] = E_X[E[Y\vert T=1, X] - E[Y\vert T=0, X]]\]