Transfer Learning and Transportability

Lecture Notes on Causal Inference

Transfer learning

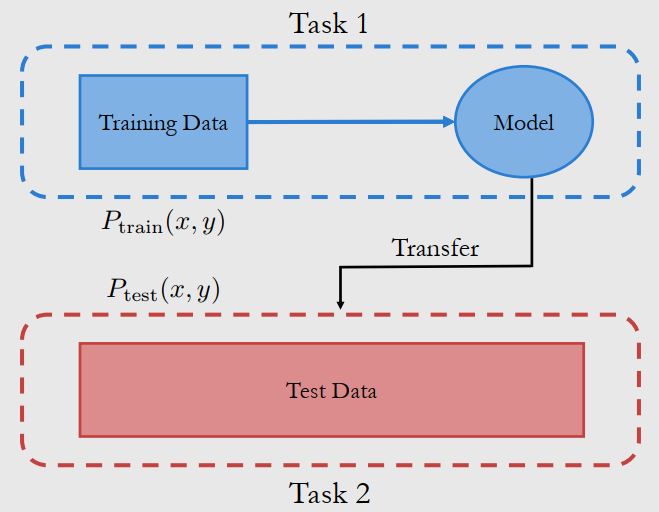
在迁移学习中，我们将任务1中由训练数据1得到的模型1迁移到任务2，帮助从训练数据2得到模型2，实际中可能有多个任务。我们在这里主要讨论的是 Domain Generalization，其框架如下
Domain Generalization

在 domain generalization中，我们设定 $P_{train}(x,y)\neq P_{test}(x,y)$ ，如果这两者相等，此时任务则退化为常规的监督学习。我们的目标是在只接触 $P_{train}(x,y)$ 时，建模 $E_{test}(Y\vert x)$ 。

在这里我们还需要做一个假设称为 Covariate Shift Assumption，即

\[P_{train}(y\vert x) = P_{test}(y \vert x) \qquad P_{train}(x)\neq P_{test}(x)\]

此外，还要求 train 和 test 的数据范围相同

在分布内预测 Y 时，我们用无结构的vector X 来预测 Y ，而我们也可以用因果结构的角度来理解预测。这时的任务为 in-distribution prediction of Y from out-of-sample data for X ，即给出 $P_{train}$ 中没有见过的 X，预测对应的落在 $P_{train}$ 中的 Y 。

那么此时最自然的一个问题是，我们最少需要多少个变量就可以得到最优的预测结果呢？这时我们需要因果图中找到 Y 的 Markov Blanket，集合内的元素就是最少需要的变量。

Markov Blanket 的目的是 block 因果图中所有节点到 Y 的path。因此它包含 Y 所有的父节点，子节点和子节点的其他父节点三类。

除了这个任务外，还有其他任务也可以从因果推理的角度理解。比如用从 $P_{test}$ 中采样得到的 X 来预测 Y。我们认为所有的 test 分布都可以看成对因果图部分节点做intervention生成。此时结合之前提到的Modularity假设，即 Intervening on a variable only changes the causal mechanism (structural equation) for that variable. All other causal mechanisms remain unchanged. 我们有结论：Causal Mechanism is Optimal in Robust Sense。当condition 包含 Y 的非父节点时，intervention on other nodes 会对最终的结果产生干扰影响。

这可以看成是对 Covariate shift 假设的放松，此时我们只要求 $P_{train}(y\vert parent(Y)) = P_{test}(y \vert parent(Y))$

Transportability of Causal Effects Across Populations

Transportability: transport causal effects across different populations
具体来说，已知源人群数据 $P(y,t,…)$ 和 目标人群数据 $P^{\star}(y,t,…)$ ，给出源模型 $P(y\vert do(t),x)$ ，我们的目标是得到对应模型 $P^{\star}(y\vert do(t),x)$ ，判断两者是否相等

我们首先引入 Selection Diagrams 的概念，它允许两个分布有不同的causal mechanism。具体方法是增加节点 S 指向原图节点。此时我们有 $P^{\star}(y \vert do(t), x) \triangleq P(y \vert do(t), x, s^{\star})$

这里有一些不同的 Transportability，列举如下