Causal Discovery from Interventions

Lecture Notes on Causal Inference

Single-Node Structural Intervention

我们首先考虑最简单的情况，即只有 A 和 B 两个变量，此时真实的因果图有三种情况：$A \rightarrow B$，$A \leftarrow B$ 和 $A \quad B$。
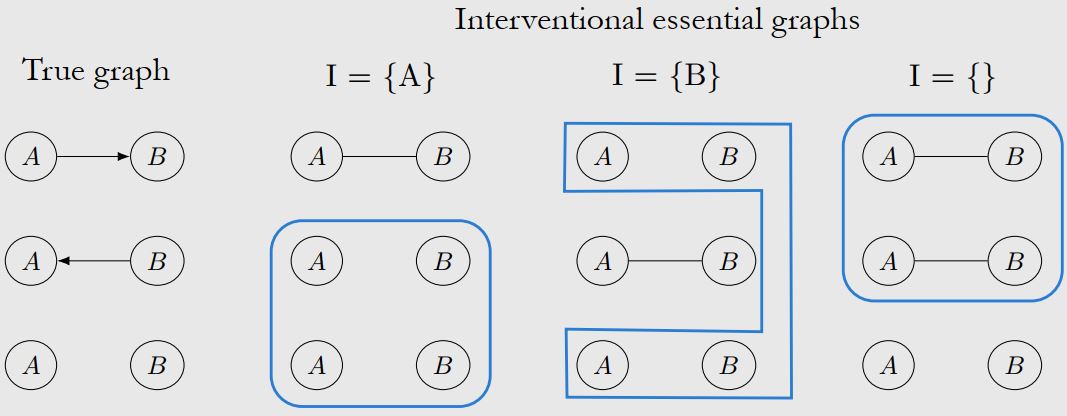
以第一种情况为例，我们可以写出 A 和 B 的结构方程，$A:=N_A$，$B:=f(A,N_B)$ 。在我们intervene B 之后，此时 B 不受 A 的影响，B 的结构方程变为 $B:=N_B’$ 。由此我们可以得到三种情况下，分别对A，B干预，或者是不干预对应的 Interventional essential graphs 如下
Interventional essential graphs
我们可以发现，如果我们只干预其中一个变量，此时我们无法确定真实的因果图。而当我们分别干预两个变量时，此时我们可以唯一确定真实的因果图。

根据已有研究，对于单变量的intervention，当变量数 n>2 时，(n-1) 次intervention足够得到真实的因果图。（注意，如果这(n-1) 次intervention中包含空intervention，即只有观测结果时，此时最差情况下我们需要n次intervention来得到因果图）

反过来同样成立，(n-1)次intervention也是必要条件，在最差情况下，我们需要(n-1)次intervention，其他情况下intervention的必需次数要少一些。

以上定理提到的最差情况是指，essential graph是完全图，任何两个节点之间都存在一条无向边

Multi-Node Structural Intervention

多节点intervention是指，在每次intervention，我们可以同时intervene on multiple nodes。
那么此时需要多少次intervention才能确定真实的因果图呢？在这里我们直接给出结论，并和单节点intervention的结论进行对比，假设节点个数为n

接下来的一个问题是，如果不是完全图这种最差情况，那么我们需要多少次intervention可以确定因果图呢？

为此我们首先引入 clique 的概念，clique 表示原图中最大的完全子图节点集合。举个例子，如果原图恰好为完全图，那么最大的clique就是图中所有节点的集合

基于clique的概念，我们有定理：在 multi-node intervention 下， $\lceil log_2(c) \rceil$ 次intervention可以得到真实因果图。这里 c 是最大clique中的节点个数

Parametric Interventions

在structural intervention中，我们的处理方式是将 $Y:=f_\theta(X,N_Y)$ 变为 $Y:=N_Y’$
而在parametric intervention中，我们的处理方式是将 $Y:=f_\theta(X,N_Y)$ 变为 $Y:=f_{\theta’}(X,N_Y)$
换言之，我们不是改变 Y 让其不依赖parent，而是改变 Y 对parent的依赖方式，即改变给定parent后 Y 的条件概率分布。所以，仅从概念上来看，parametric intervention包含了structural intervention。但实际上我们称呼 parametric intervention 是指原集合除去 structural intervention 后的部分。除此之外，这两种intervention 方式还有一些其他称呼，比如 hard vs. soft，perfect vs. imperfect

在单节点干预下，parametric intervention和structural intervention的结论相同，即 (n-1) 次intervention是充要条件

这引出了下一个问题，当我们采取少于 (n-1) 次intervention时，我们得到的是什么样的结果，即怎样的图呢？

在单节点的干预下，我们每次intervention，都会引入 immorality。当采取少于 (n-1) 次intervention时，我们会得到部分边有方向，部分边无向的图。
我们有定理：Two graphs augmented with single-node interventions are interventionally Markov equivalent if any only if they have the same skeletons and immoralities

在多节点的干预下，我们有类似的定理：Given the observational data, two graphs augmented with multinode interventions are interventionally Markov equivalent if and only if they have the same skeletons and immoralities

Miscellaneous Other Settings

这里列举一些其他情况下的处理方法及研究