Intro to Causal Inference

Lecture Notes on Causal Inference

Introduction

This blog is based on courses from Brady Neal
Website: https://www.bradyneal.com/causal-inference-course

Simpson’s paradox

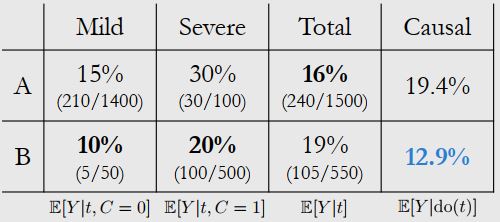
针对疫情，假设我们有两种药A(0)和B(1)，病人的情况分为mild(0)和severe(1)，最后治疗的结果为alive(0)和dead(1)两种情况。具体死亡率如下表
在这个例子中，如果只看总死亡率，那么A的效果要更好。但如果分别看不同症状下的死亡率，则B的表现均比A好，这就是Simpson’s paradox
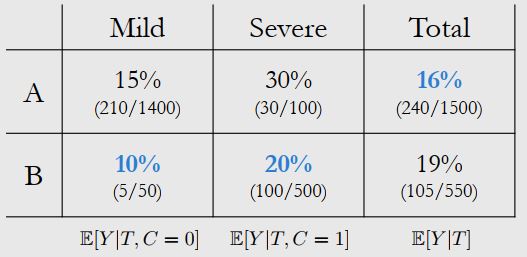
那么到底哪种药更好呢？这取决于causal structure

• 如果病人情况同时会对治疗方式和最终结果产生影响，则 B 这种药更好。从定性的角度来分析，B 这种药被不平等地分配给重症患者更多
• 如果是治疗方式同时对病人情况和最终结果产生影响，则 A 这种药更好。如果确定使用 B ，因为其稀缺性，患者可能会在等待中从mild变为severe

Correlation does not imply causation

我们发现穿鞋睡觉和起床头疼之间有很大的相关性，但这两者之间并不是causation的关系。这是因为这两个现象由一个共同的原因导致，那就是睡前饮酒。为此我们有两种解释

• 穿鞋睡觉与不穿鞋睡觉这两类人差异很大(不平等的初始采样)。意思是说，穿鞋睡觉的大部分人都是喝醉的，而不穿鞋的大部分都是清醒的
• Confounding：若存在潜在原因 C 同时导致 A 和 B 现象的产生，则说 A 和 B 之间是confounding association
  而全局的联系 (e.g. correlation)可看成mixture of causal and confounding association

那么这种 Correlation = Causation 的认知偏差从何而来呢？

• Availability heuristic：比如最近看到文章说睡前喝咖啡会头疼，因此误认为喝咖啡是一个导致头疼的原因
• Motivated reasoning：比如不得不见老丈人，要做自己不喜欢的事。因此认为老丈人导致的头疼

What does imply causation?

这里需要引入一个新的概念，potential outcome，比如吃药会让头不疼
Notation

• T: observed treatment，在这个例子中为是否吃药
• Y: observed outcome，在这个例子中为头疼是否缓解
• i: 表示一个特殊单位或独立个体，在这个例子中为某个头疼的人
• \(Y_{i \vert do(T=1)} \triangleq Y_i(1)\): potential outcome under treatment，吃药的结果
• \(Y_{i \vert do(T=0)} \triangleq Y_i(0)\): potential outcome under no treatment，不吃药的结果

基于这些表示，我们定义 Causal effect = \(Y_i(1)-Y_i(0)\)
这引出了因果推理中最根本的问题，对于一个独立个体而言，我们无法得到causal effect。因为我们只能观察到一种结果，不能再回头去做另外的决定。在例子中，对于个体而言，他只能从吃药和不吃药两种决定中选择一个，也就无法观察到另一种决定导致的可能结果。

为此我们用统计意义上群体的平均来代替个体，Average treatment effect (ATE):

\[E[Y_i(1)-Y_i(0)] =E[Y(1)]-E[Y(0)]\neq E[Y|T=1]-E[Y|T=0]\]

这个不等号的原因就是\(Correlation \neq Causation\)，在Y和T之间还存在着confounding association。换个角度来看，如果我们能去掉所有潜在的原因，那么我们就可以将不等号变为等号

其中一种可采用的方法就是随机化，Randomized control trials (RCTs)。在例子中，我们为了消除睡前饮酒这个confounding，我们可以通过抛硬币来决定是否给睡着的人穿上鞋子(或者脱掉)。这样的话，睡前饮酒这个原因就无法对我们的因果推理产生影响。
即通过RCTs，我们可以去掉潜在关联，让不同组之间具有可比性。

Causation in observational studies

但在我们的生活中，很多时候我们不能保证消除潜在因素，也不能进行随机化处理，尤其是在观察学习中。比如在吸烟和肺癌的数据集中，我们显然不能完全随机化强迫个体吸烟。而对于机器学习的数据集，我们甚至不能保证其数据的采样是完全随机的。

为此，我们的处理方法是adjust/control for confounders，用条件分布+期望去边缘化(block)潜在因素，即 \(E[Y|do(T=t)]=E_CE[Y|t,C]\)，回到开头的那个例子，假设患者病情同时影响治疗方式和最终结果，那么我们可以计算出实际的死亡率